삼각함수와 미적분을 마스터하다
수학으로 배우는
파동의 법칙
Transnational College of LEX 지음
이경민 옮김
Gbrain 펴냄
2013.10.9.
세상의 모든 것은 파동이다.
내 심장의 규칙적인 움직임도, 빛도, 소리도 파동이다. 푸리에 해석은 그런 파동을 해석하는 수학적 기법이다. 이 책은 푸리에 급수와 푸리에 계수에 대해 아주 쉽게 설명한다. 그도 그럴 것이 이 책은 초등학생과 중학생이 포함된 수학 스터디 그룹이 만든 공동 기획물이다. 푸리에 해석을 어떻게 하면 쉽게 이해하고 설명할 수 있을까 함께 고민하고 함께 모니터링 하면서 만든 저작물이다. 일본에서 만들어졌지만 여러 나라에서 공식 교과서로 사용되고 있다고 한다. 그럴만 하게 내용이 좋다.
나는 수학을 너무 압축적으로 배웠다.
수식으로만 증명했고 정제된 공식만 외웠다. 이책은 삼각함수의 적분을 설명하면서 가위와 풀로 삼각함수의 그래프를 오려 붙여가며 한주기 동안의 삼각함수 적분이 0 임을 설명한다. 단순한 시도지만 수식만으로는 느낄 수 없는 생생한 직관을 얻었다. 논어에 학이불사즉망(學而不思則罔)이라는 구절이 있다. 배우기만 하고(學而) 생각할 여유가 없었기 때문에(不思) 나는 수학에서 망했던 것이다(則罔).
이 책의 하일라이트는
삼각함수로 구성된 푸리에 해석에 오일러 공식을 적용해서 간결한 복소수 표현으로 바꾸는 과정을 설명하는 부분이다. 복소평면과 삼각함수 사이의 관계를 표현하는 오일러 공식과, 모든 함수를 일관된 형태로 표현하는 매클로린 전개를 이용해서 푸리에 급수를 아름답도록 간결한 표현으로 바꾸어가는 과정을 멋드러지게 설명한다.
저술과 번역 모두 좋았다.
 |
 |
2024.6.3.
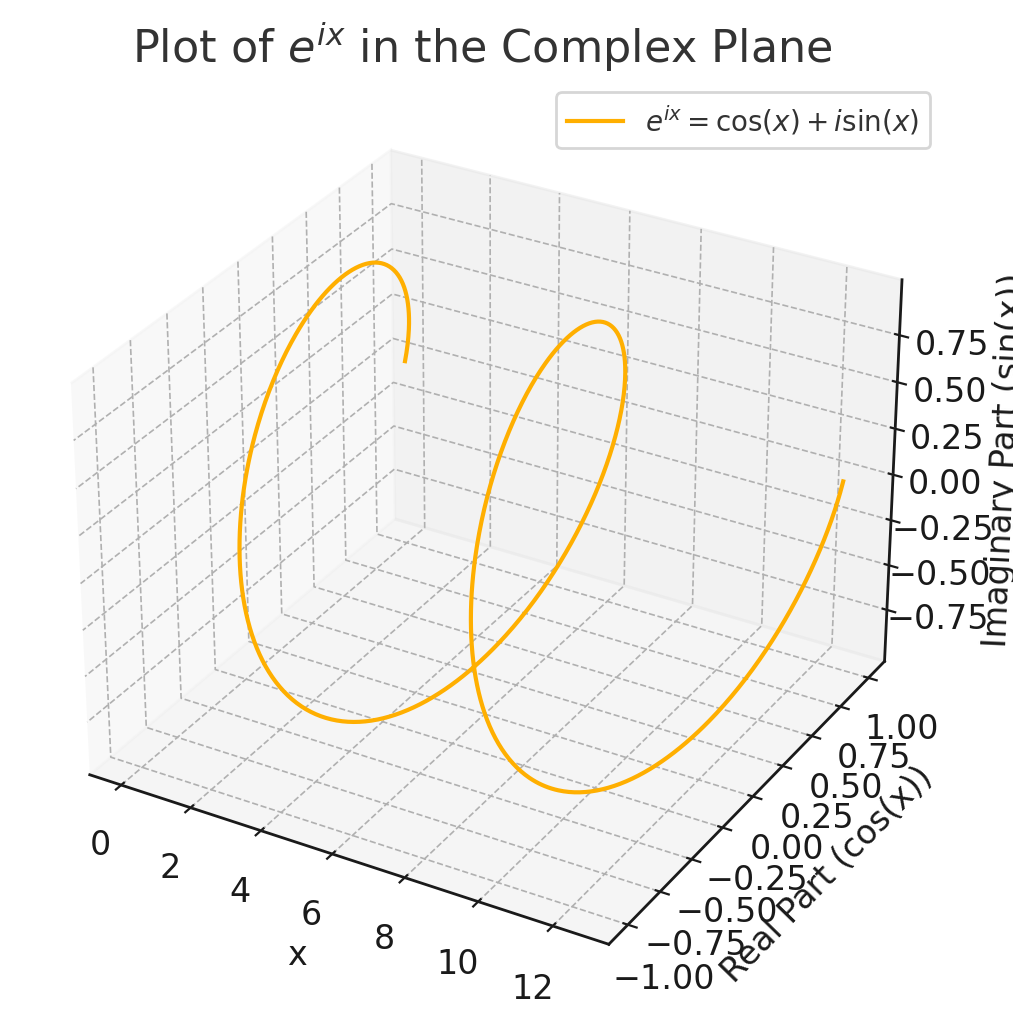
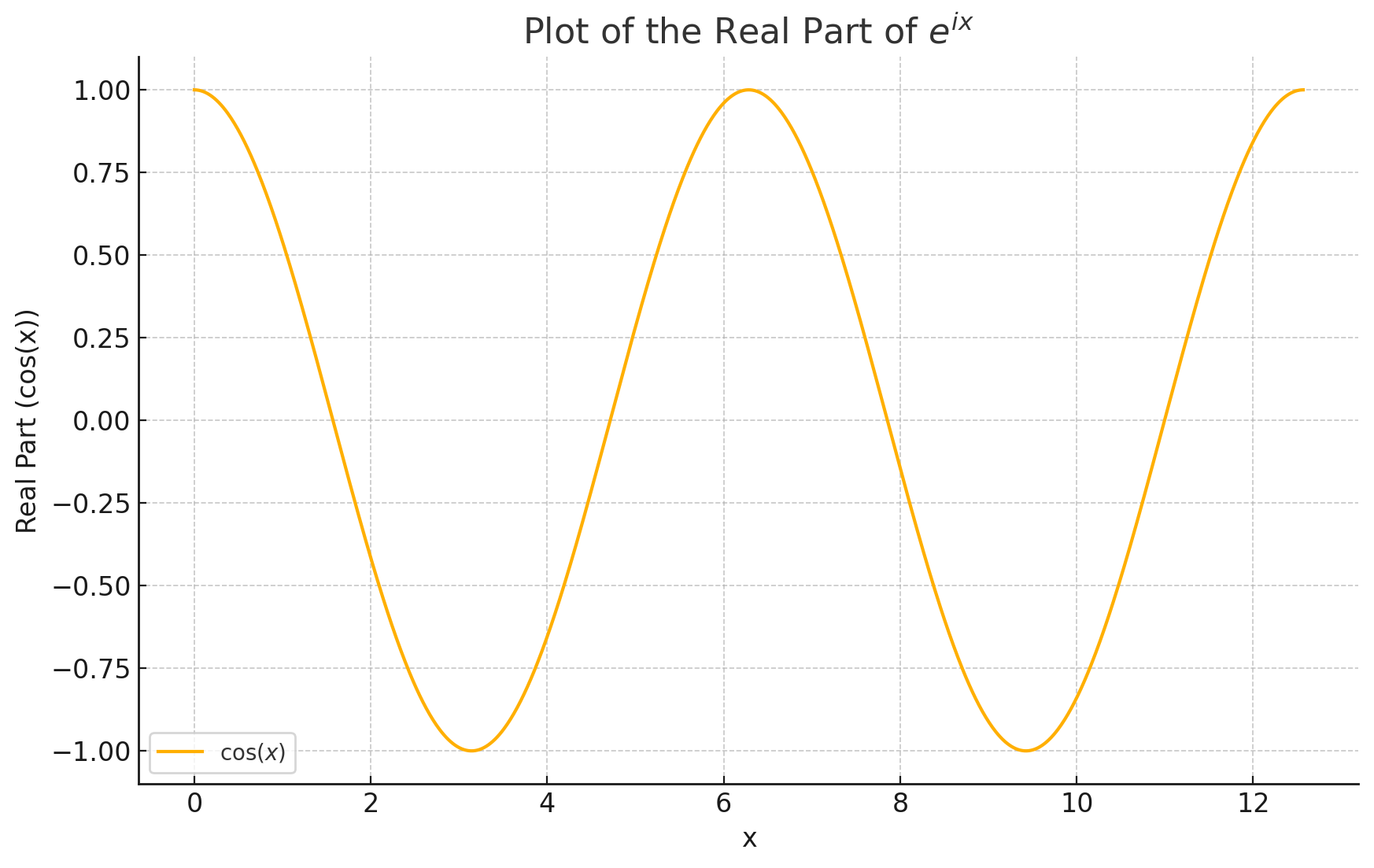
이제 e의 복소지수 수식을 보면 그 이면의 코사인 함수와 사인 함수가 보인다. 오일러 공식과 친해진 것이다. 기쁘다.
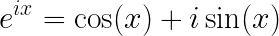
독서를 통해 푸리에 급수가 무엇인지, 푸리에 변환이 무엇인지 흡족하게 배웠다. 그 과정에서 미분과 적분도 충분히 연습했다. 대학 전공 공부 전에 이 책을 봤다면 공업수학 빵구는 면했을 것이다. 아쉽다.
훌륭한 번역이었다 (번역 별 3.5 ★★★☆).


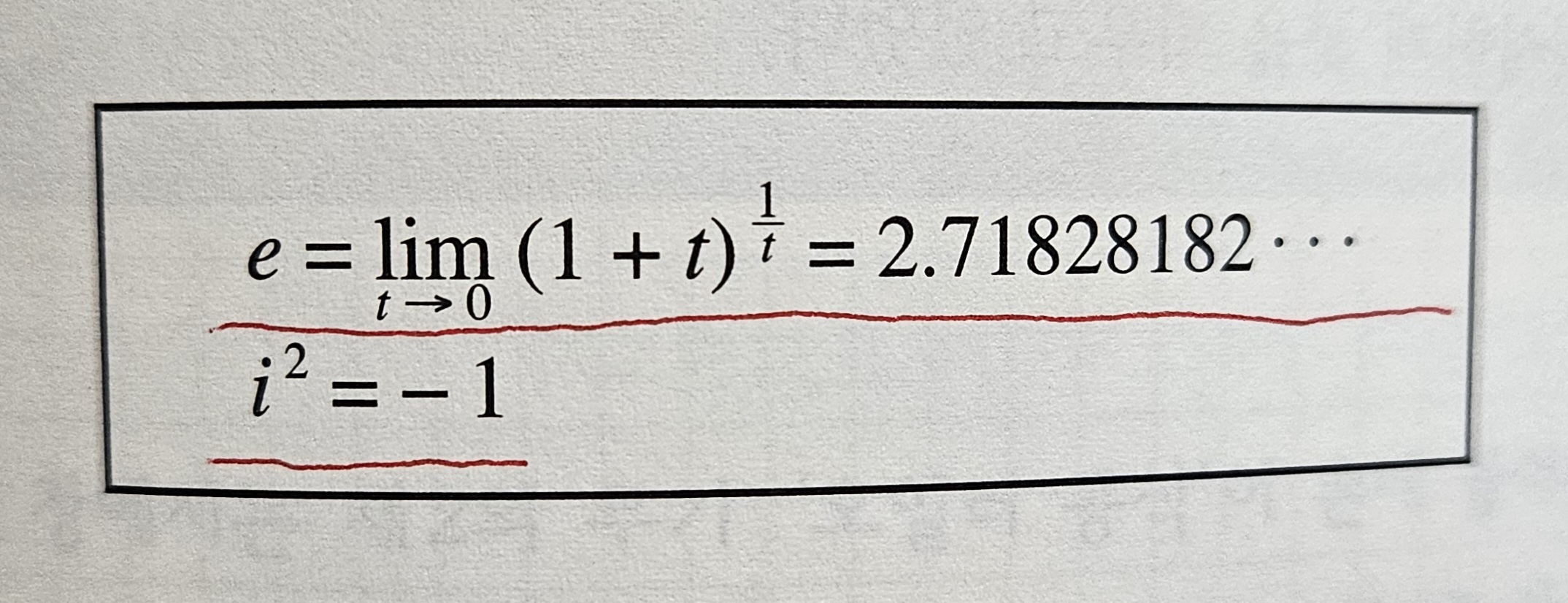

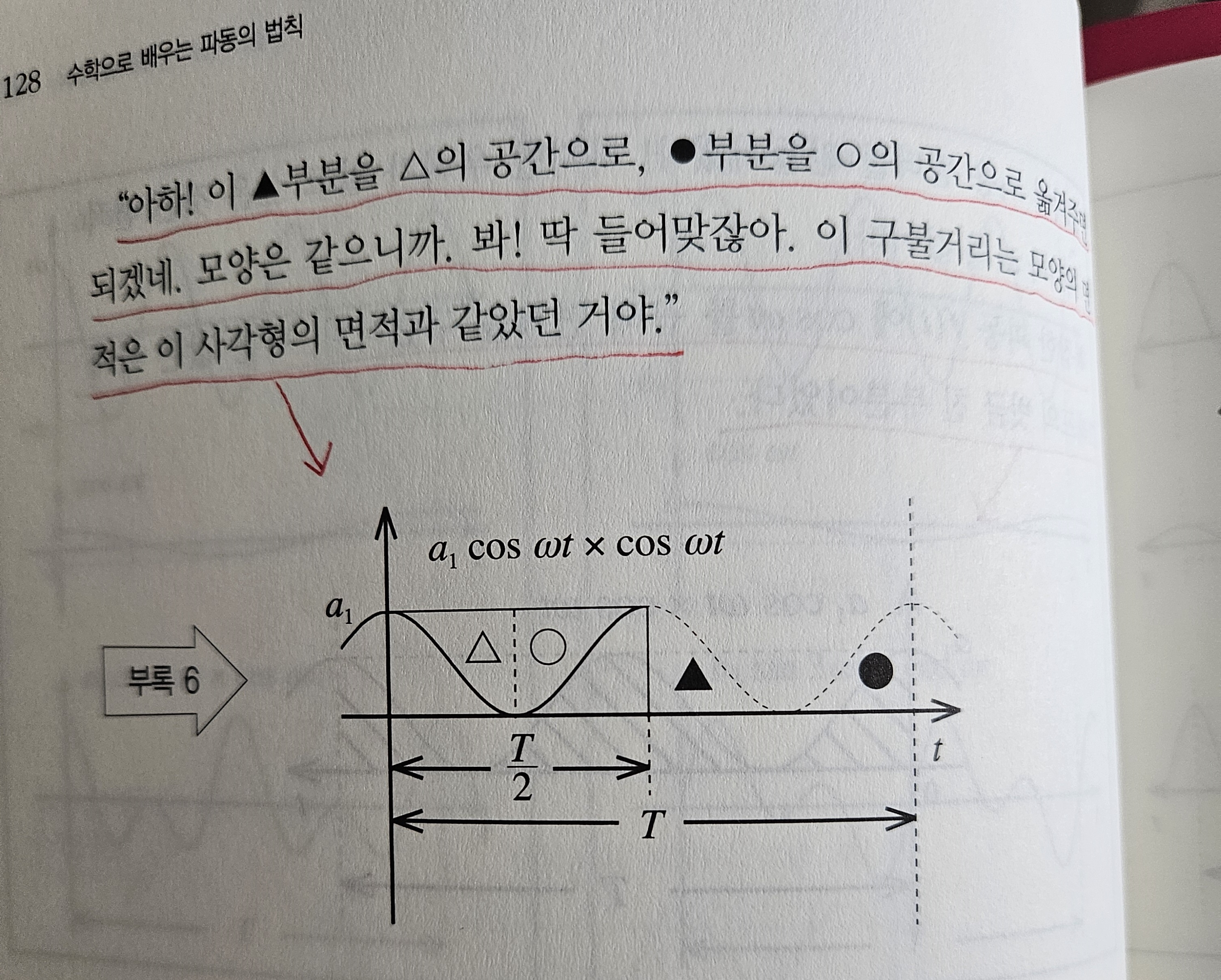
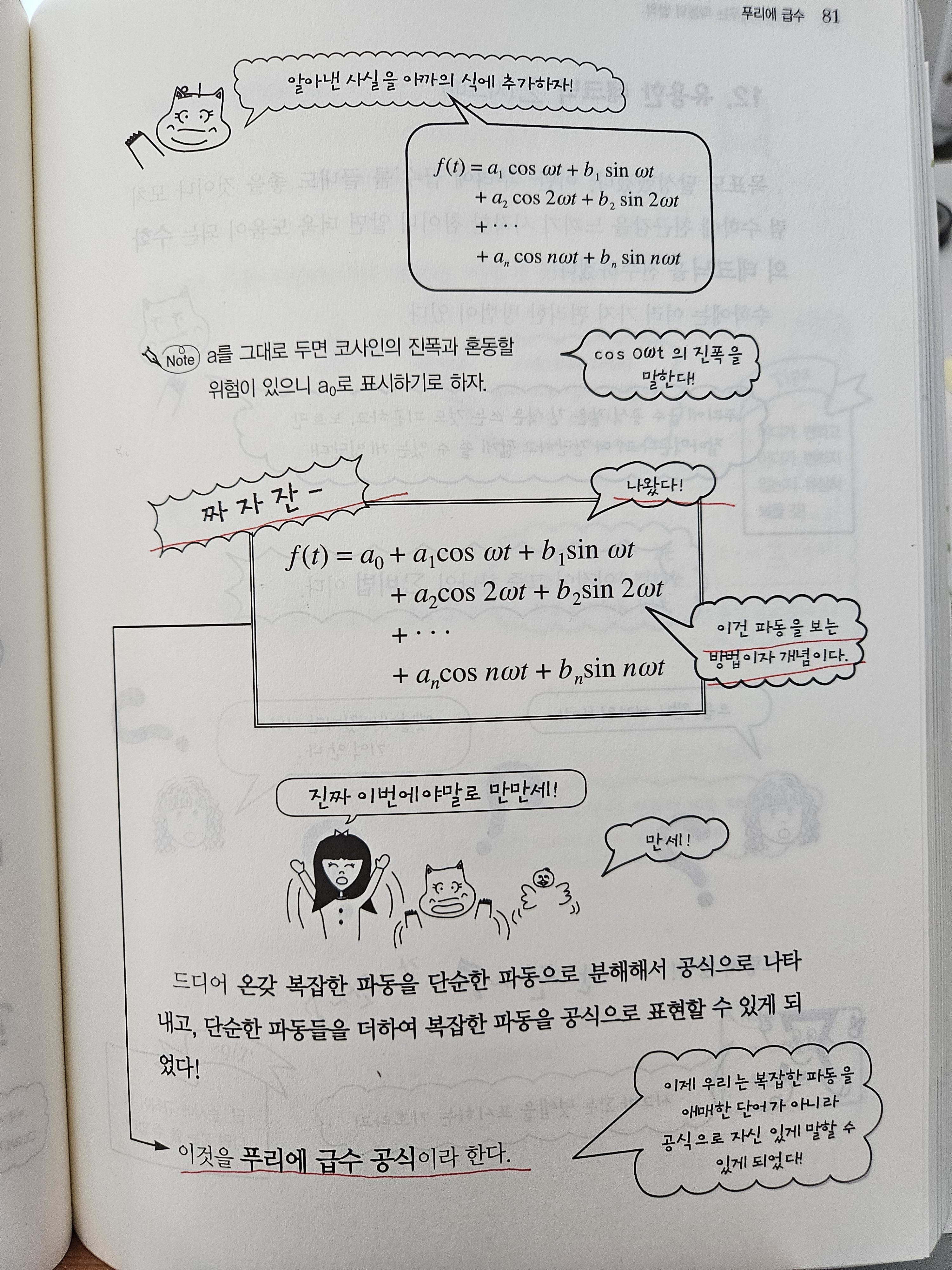
독서를 마칠 때 쯤 ChatGPT가 그려준 그림을 보고 많은 것을 생각했다. 그림을 보고 생각해야 더 생생하게 각인되는 무엇이 있는 것 같다. ChatGPT가 제시한 그림이 독서를 정리하는데 도움됐다.